 |
| Om Epimenides |
Ada yang pernah dengar tentang paradoks pembohong nggak? Saya yakin sebagian dari kita sudah pernah mendengarnya. Sekedar untuk refreshing otak, saya akan ungkit kembali tentang paradoks ini. Paradoks pembohong adalah paradoks yang sangat tua dan terkenal yang diungkapkan oleh seorang pria Yunani, Epimenides, sekitar abad 6 SM. Tapi sebelum ane lanjut pada paradoks pembohong, terlebih dahulu kita cari tahu apa itu paradoks.
Menurut kamus besar bahasa indonesia, paradoks adalah sesuatu pernyataan yg seolah-olah bertentangan (berlawanan) dng pendapat umum atau kebenaran, tetapi kenyataannya mengandung kebenaran.
Sedangkan menurut wikipedia, Paradoks adalah suatu situasi yang timbul dari sejumlah premis yang diakui kebenarannya yang bertolak dari suatu pernyataan dan akan tiba pada suatu konflik atau kontradiksi.
Well, karena kita udah tau pengertian paradoks, kita lanjut ke paradoks pembohong. Paradoks itu mengatakan
“Epimenides si orang Kreta mengatakan bahwa semua orang Kreta adalah pembohong.”
Mengapa pernyataan ini merupakan suatu paradoks? Karena pernyataan tersebut membawa kita pada dua kesimpulan yang bertentangan satu sama lain.
Perhatikan premis berikut.
1. Jika yang dikatakan Epimenides benar, berarti dia bukan pembohong.
2. Jika Epimenides bukan pembohong, berarti apa yang dia katakan tidak benar.
3. Jika apa yang dikatakannya tidak benar, berarti dia pembohong.
Kesimpulannya, epimenides adalah pembohong.
Premis Kedua:
1. Jika yang dikatakan epimenides tidak benar, berarti dia pembohong.
2. Jika epimenides bukan pembohong, berarti apa yang dia katakan benar.
3. Jika apa yang dikatakannya tidak benar, berarti dia bukan pembohong, karena dia orang Kreta.
Kesimpulannya, Epimenides bukan pembohong.
Jelas dari kedua kesimpulan tersebut kita tau bahwa pernyataan Epimenides mengandung dua nilai kebenaran, yaitu benar dan salah. Tapi kenapa bisa begitu? Apa mungkin suatu hal bisa benar sekaligus salah?
Memang itulah kenyataannya. Di dunia ini memang banyak hal yang membingungkan. Banyak hal yang menurut kita salah, tapi ternyata benar. Dan sebaliknya, sesuatu yang kita anggap benar ternyata salah. so, bersikap bijaklah dalam menyikapi sesuatu. Jangan terlampau mudah menerima sesuatu sebagai kebenaran atau kesalahan. Dan jangan pula terlalu arogan untuk menerima sesuatu kebenaran atau menolak kesalahan jika kenyataanya ia benar atau ia salah. : )
 habis dibagi 7, maka
habis dibagi 7, maka 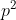 habis dibagi 7. Berakibat p juga habis dibagi 7. Artinya terdapat bilangan bulat k sehingga berlaku
habis dibagi 7. Berakibat p juga habis dibagi 7. Artinya terdapat bilangan bulat k sehingga berlaku  Dengan demikian, diperoleh
Dengan demikian, diperoleh habis dibagi 7, maka
habis dibagi 7, maka  juga habis dibagi 7. Akibatnya q juga habis dibagi 7. Karena p dan q sama-sama habis dibagi 7, maka p dan q memiliki faktor persekutuan selain 1, yaitu 7. Terjadi kontradiksi dengan pernyataan semula bahwa p dan q tidak memiliki faktor persekutuan selain 1. Berarti pengandaian salah sehingga terbukti bahwa
juga habis dibagi 7. Akibatnya q juga habis dibagi 7. Karena p dan q sama-sama habis dibagi 7, maka p dan q memiliki faktor persekutuan selain 1, yaitu 7. Terjadi kontradiksi dengan pernyataan semula bahwa p dan q tidak memiliki faktor persekutuan selain 1. Berarti pengandaian salah sehingga terbukti bahwa 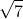 adalah bilangan irrasional. QED
adalah bilangan irrasional. QED